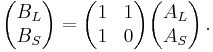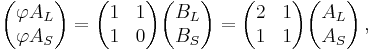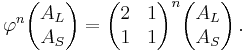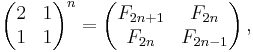Penrose tiling

A Penrose tiling.

A Penrose tiling is a nonperiodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. Because all tilings obtained with the Penrose tiles are non-periodic, Penrose tiles are considered aperiodic tiles. A Penrose tiling may be constructed so as to exhibit both reflection symmetry and fivefold rotational symmetry, as in the diagram at the right.

A Penrose tiling has many remarkable properties, most notably:

It is nonperiodic, which means that it lacks any translational symmetry. More informally, a shifted copy will never match the original exactly.
Any finite region in a tiling appears infinitely many times in that tiling and, in fact, in any other tiling. This property would be trivially true of a tiling with translational symmetry but is non-trivial when applied to the non-periodic Penrose tilings.
It is a quasicrystal: implemented as a physical structure a Penrose tiling will produce Bragg diffraction; the diffractogram reveals both the underlying fivefold symmetry and the long range order. This order reflects the fact that the tilings are organized, not through translational symmetry, but rather through a process sometimes called "deflation" or "inflation."

Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions, cut and project schemes and coverings.

Roger Penrose in the foyer of the Mitchell Institute for Fundamental Physics and Astronomy, Texas A&M University, standing on a floor with a Penrose tiling.

Background and history

Periodic and aperiodic tilings

Figure 1. Part of a periodic tiling.

Penrose tilings are simple examples of aperiodic tilings of the plane.^[1] A tiling is a covering of the plane by tiles with no overlaps or gaps; the tiles normally have a finite number of shapes, called prototiles, and a set of prototiles is said to admit a tiling or tile the plane if there is a tiling of the plane using only tiles congruent to these prototiles.^[2] The most familiar tilings (e.g., by squares or triangles) are periodic: a perfect copy of the tiling can be obtained by translating all of the tiles by a fixed distance in a given direction. Such a translation is called a period of the tiling; more informally, this means that the tiling repeats itself. If a tiling has no periods it is said to be nonperiodic. A set of prototiles is said to be aperiodic if it tiles the plane, but every such tiling is nonperiodic; tilings by aperiodic sets of prototiles are called aperiodic tilings.^[3]

Earliest aperiodic tilings

An aperiodic set of Wang dominoes.^[4]

The subject of aperiodic tilings received new interest in the 1960s when logician Hao Wang noted connections between decision problems and tilings.^[5] In particular, he introduced tilings by square plates with colored edges, now known as Wang dominoes or tiles, and posed the "Domino Problem": to determine whether a given set of Wang dominoes could tile the plane with matching colors on adjacent domino edges. He observed that if this problem were undecidable, then there would have to exist an aperiodic set of Wang dominoes. At the time, this seemed implausible, so Wang conjectured no such set could exist.

Robinson's six prototiles.

Wang's student Robert Berger proved that the Domino Problem was undecidable (so Wang's conjecture was false) in his 1964 thesis,^[6] and obtained an aperiodic set of 20426 Wang dominoes.^[7] He also described a reduction to 104 such prototiles; the latter did not appear in his published monograph,^[8] but in 1968, Donald Knuth detailed a modification of Berger's set requiring only 92 dominoes.^[9]

The color matching required in a tiling by Wang dominoes can easily be achieved by modifying the edges of the tiles like jigsaw pieces so that they can only fit together as prescribed by the edge colorings.^[10] Raphael Robinson, in a 1971 paper^[11] which simplified Berger's techniques and undecidability proof, used this technique to obtain an aperiodic set of just six prototiles.^[12]

Development of the Penrose tilings

Figure 2. The pentagonal Penrose tiling (P1) drawn in black on a colored rhombus tiling (P3) with yellow edges.^[13]

The first Penrose tiling (tiling P1 below) is also an aperiodic set of six prototiles, introduced by Roger Penrose in a 1974 paper,^[14] but is based on pentagons rather than squares. Attempts to tile the plane with regular pentagons necessarily leave gaps, but Johannes Kepler had shown in his 1619 work Harmonices Mundi that these gaps could be filled using pentagrams (viewed as star polygons), decagons and related shapes.^[15] Acknowledging inspiration from Kepler, Penrose was able to find matching rules (which can be imposed by decorations of the edges) for these shapes to obtain an aperiodic set; his tiling can be viewed as a completion of Kepler's finite Aa pattern,^[16] and other traces of these ideas can be found in Albert Dürer's work.^[17]

Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below).^[18] The rhombus tiling was independently discovered by Robert Ammann in 1976.^[19] Penrose and John H. Conway investigated the properties of Penrose tilings and discovered that a substitution property explained their hierarchical nature; their findings were publicized by Martin Gardner in his January 1977 "Mathematical Games" column in Scientific American.^[20]

In 1981 De Bruijn explained a method to construct Penrose tilings^[21] from five families of parallel lines as well as a "cut and project method", in which Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In this approach, the Penrose tiling is viewed as a set of points, its vertices, while the tiles are geometrical shapes obtained by connecting vertices with edges.

The Penrose tilings

A P1 tiling using Penrose's original set of six prototiles.

The three types of Penrose tiling P1–P3 are described individually below.^[22] They have many common features: in each case the tiles are constructed from shapes related to the pentagon (and hence the golden ratio), but the basic tile shapes need to be supplemented by matching rules in order to tile aperiodically; these rules may be described using labeled vertices or edges, or patterns on the tile faces – alternatively the edge profile can be modified (e.g. by indentations and protrusions) to obtain an aperiodic set of prototiles.^[7]^[23]

The original pentagonal Penrose tiling (P1)

Penrose's first tiling uses pentagons and three other shapes: a five-pointed "star" (a pentagram), a "boat" (roughly 3/5 of a star) and a "diamond" (a thin rhombus).^[24] To ensure that all tilings are nonperiodic, there are matching rules that specify how tiles may meet each other, and there are three different types of matching rule for the pentagonal tiles. It is common to indicate the three different types of pentagonal tiles using three different colors, as in the figure above right.^[25]

Kite and dart tiling (P2)

Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus; however, the matching rules prohibit such a combination.^[26] Both the kite and dart are composed of two triangles, called Robinson triangles, after 1975 notes by Robinson.^[27]

Kite and dart tiles (top) and the seven possible vertex figures in a P2 tiling.

The kite is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
The dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.

The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices.^[28] Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.^[18]

These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way.^[29] Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact there are only seven possible ways for the tiles to meet at a vertex; two of these figures, namely the "star" (top left) and the "sun" (top right), have 5-fold dihedral symmetry (by rotations and reflections) while the remainder have a single axis of reflection (vertical in the image).^[30] All of these vertex figures apart from the ace and the sun force the placement of additional tiles.^[31]

Rhombus tiling (P3)

Matching rule for Penrose rhombs using circular arcs or edge modifications.

The third tiling uses a pair of rhombuses (often referred to as "rhombs" in this context) with equal sides but different angles.^[7] Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled: no two tiles may form a parallelogram, as this would allow a periodic tiling, but this constraint is not sufficient to force aperiodicity, as figure 1 above shows.

There are two kinds of tile, both of which can be decomposed into Robinson triangles.^[27]

The thin rhomb t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhomb may be bisected along its short diagonal to form a pair of acute Robinson triangles.
The thick rhomb T has angles of 72, 108, 72, and 108 degrees. The T rhomb may be bisected along its long diagonal to form a pair of obtuse Robinson triangles; in contrast to the P2 tiling, these are larger than the acute triangles.

The matching rules distinguish sides of the tiles and require that tiles can only be adjacent in particular ways. Two ways to describe these matching rules are shown in the image on the right: tiles must be assembled so that the curves on the faces match in color and position across an edge; alternatively tiles must be assembled so that the bumps on their edges fit together.^[7]

There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only seven of these combinations to appear, although one of these arises in two ways.^[32]

Features and constructions

The golden ratio and local pentagonal symmetry

Several properties and common features of the Penrose tilings involve the golden ratio φ = (1+√5)/2 (approximately 1.618).^[28]^[27] This is the ratio of chord lengths to side lengths in a regular pentagon, and satisfies φ = 1 + 1/φ.

Pentagon with an inscribed thick rhomb (light), acute Robinson triangles (lightly shaded) and a small obtuse Robinson triangle (darker). Dotted lines give additional edges for inscribed kites and darts.

Consequently, the ratio of the lengths of long sides to short sides in the (isosceles) Robinson triangles is φ:1. It follows that the ratio of long side lengths to short in both kite and dart tiles is also φ:1, as are the length ratios of sides to the short diagonal in the thin rhomb t, and of long diagonal to sides in the thick rhomb T. In both the P2 and P3 tilings, the ratio of the area of the larger Robinson triangle to the smaller one is φ:1, hence so are the ratios of the areas of the kite to the dart, and of the thick rhomb to the thin rhomb. (Both larger and smaller obtuse Robinson triangles can be found in the pentagon on the right: the larger triangles at the top – the halves of the thick rhomb – have linear dimensions scaled up by φ compared to the small shaded triangle at the base, and so the ratio of areas is φ²:1.)

Any Penrose tiling has local pentagonal symmetry, in the sense that there are points in the tiling surrounded by a symmetric configuration of tiles: such configurations have fivefold rotational symmetry about the center point, as well as five mirror lines of reflection symmetry passing through the point, a dihedral symmetry group.^[7] This symmetry will generally preserve only a patch of tiles around the center point, but the patch can be very large: Conway and Penrose proved that whenever the colored curves on the P2 or P3 tilings close in a loop, the region within the loop has pentagonal symmetry, and furthermore, in any tiling, there are at most two such curves of each color which do not close up.^[33]

There can be at most one center point of global fivefold symmetry: if there were more than one, then rotating each about the other would yield two closer centers of fivefold symmetry, which leads to a mathematical contradiction.^[34] There are only two Penrose tilings (of each type) with global pentagonal symmetry: for the P2 tiling by kites and darts, the center point is either a "sun" or "star" vertex.^[35]

Inflation and deflation

A pentagon decomposed into six smaller pentagons (half a dodecahedral net) with gaps.

Many of the common features of Penrose tilings follow from a hierarchical pentagonal structure given by substitution rules: this is often referred to as inflation and deflation, or composition and decomposition, of tilings or (collections of) tiles.^[20]^[7]^[36] The substitution rules decompose each tile into smaller tiles of the same shape as those used in the tiling (and thus allow larger tiles to be "composed" from smaller ones).

Penrose originally discovered the P1 tiling in this way, by decomposing a pentagon into six smaller pentagons (one half of a net of a dodecahedron) and five half-diamonds; he then observed that when he repeated this process the gaps between pentagons could all be filled by stars, diamonds, boats and other pentagons.^[37] By iterating this process indefinitely he obtained one of the two P1 tilings with pentagonal symmetry.^[7]^[16]

Robinson triangle decompositions

Robinson triangles and their decompositions.

The substitution method for both P2 and P3 tilings can be described using Robinson triangles of different sizes. The Robinson triangles arising in P2 tilings (by bisecting kites and darts) are called A-tiles, while those arising in the P3 tilings (by bisecting rhombs) are called B-tiles.^[27] The smaller A-tile, denoted A_S, is an obtuse Robinson triangle, while the larger A-tile, A_L, is acute; in contrast, a smaller B-tile, denoted B_S, is an acute Robinson triangle, while the larger B-tile, B_L, is obtuse.

Concretely, if A_S has side lengths (1, 1, φ), then A_L has side lengths (φ, φ, 1). B-tiles can be related to such A-tiles in two ways:

If B_S has the same size as A_L then B_L is an enlarged version φA_S of A_S, with side lengths (φ, φ, φ²=1+φ) – this decomposes into an A_L tile and A_S tile joined along a common side of length 1.
If instead B_L is identified with A_S, then B_S is a reduced version (1/φ)A_L of A_L with side lengths (1/φ,1/φ,1) – joining a B_S tile and a B_L tile along a common side of length 1 then yields (a decomposition of) an A_L tile.

In these decompositions, there appears to be an ambiguity: Robinson triangles may be decomposed in two ways, which are mirror images of each other in the (isosceles) axis of symmetry of the triangle. In a Penrose tiling, this choice is fixed by the matching rules – furthermore, the matching rules also determine how the smaller triangles in the tiling compose to give larger ones.^[27]

Partial inflation of star to yield rhombs, and of a collection of rhombs to yield an ace.

It follows that the P2 and P3 tilings are mutually locally derivable: a tiling by one set of tiles can be used to generate a tiling by another – for example a tiling by kites and darts may be subdivided into A-tiles, and these can be composed in a canonical way to form B-tiles and hence rhombs.^[13] The P2 and P3 tilings are also both mutually locally derivable with the P1 tiling (see figure 2 above).^[38]

The decomposition of B-tiles into A-tiles may be written

B_S = A_L, B_L = A_L + A_S

(assuming the larger size convention for the B-tiles), which can be summarized in a substitution matrix equation:^[39]

$\begin{pmatrix} B_L \\ B_S\end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} A_L \\ A_S \end{pmatrix}\, .$

Combining this with the decomposition of enlarged φA-tiles into B-tiles yields the substitution

$\begin{pmatrix} \varphi A_L \\ \varphi A_S\end{pmatrix} = \begin{pmatrix} 1 & 1 \\ 1 & 0 \end{pmatrix} \begin{pmatrix} B_L \\ B_S\end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}\begin{pmatrix} A_L \\ A_S \end{pmatrix}\, ,$

so that the enlarged tile φA_L decomposes into two A_L tiles and one A_S tiles. The matching rules force a particular substitution: the two A_L tiles in a φA_L tile must form a kite – thus a kite decomposes into two kites and a two half-darts, and a dart decomposes into a kite and two half-darts.^[40]^[41] Enlarged φB-tiles decompose into B-tiles in a similar way (via φA-tiles).

Composition and decomposition can be iterated, so that, for example

$\varphi^n\begin{pmatrix} A_L \\ A_S\end{pmatrix} = \begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}^n\begin{pmatrix} A_L \\ A_S \end{pmatrix}\, .$

The number of kites and darts in the nth iteration of the construction is determined by the nth power of the substitution matrix:

$\begin{pmatrix} 2 & 1 \\ 1 & 1 \end{pmatrix}^n = \begin{pmatrix} F_{2n+1} & F_{2n} \\ F_{2n} & F_{2n-1} \end{pmatrix}\, ,$

where F_n is the nth Fibonacci number. The ratio of numbers of kites to darts in any sufficiently large P2 Penrose tiling pattern therefore tends to the golden ratio φ.^[42] A similar result holds for the ratio of the number of thick rhombs to thin rhombs in the P3 Penrose tiling.^[43]

Deflation for P2 and P3 tilings

Starting with a collection of tiles from a given tiling (which could be a single tile, a tiling of the plane, or any other collection) deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with one or more new tiles, which are scaled-down versions tiles in the tiling and cover the tiles in the collection. The substitution rules guarantee that the new tiles are arranged according to the matching rules.^[40] Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.

Name	Initial tiles	Generation 1	Generation 2	Generation 3
Half-kite
Half-dart
Sun
Star

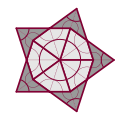Consequences and applications

Inflation and deflation yield a method for constructing kite and dart (P2) tilings, or rhombus (P3) tilings, known as up-down generation.^[29]^[40]^[44]

The Penrose tilings, being non-periodic, have no translational symmetry – the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore, a finite patch cannot differentiate between the uncountably many Penrose tilings, nor even determine which position within the tiling is being shown.^[45]

This shows in particular that the number of distinct Penrose tilings (of any type) is uncountably infinite. Up-down generation yields one method to parameterize the tilings, but other methods use Ammann bars, pentagrids, or cut and project schemes.^[40]

Notes

↑ General references for this article include Gardner 1997, pp. 1–30, Grünbaum & Shephard 1987, pp. 520–548 & 558–579, and Senechal 1996, pp. 170–206.
↑ Grünbaum & Shephard 1987, pp. 20, 23
↑ Grünbaum & Shephard 1987, p. 520
↑ Culik & Kari 1997
↑ Wang 1961
↑ Robert Berger at the Mathematics Genealogy Project
↑ ^7.0 ^7.1 ^7.2 ^7.3 ^7.4 ^7.5 ^7.6 Austin 2005a
↑ Berger 1966
↑ Grünbaum & Shephard 1987, p. 584
↑ Gardner 1997, p. 5
↑ Robinson 1971
↑ Grünbaum & Shephard 1987, p. 525
↑ ^13.0 ^13.1 Senechal 1996, pp. 173–174
↑ Penrose 1974
↑ Grünbaum & Shephard 1987, section 2.5
↑ ^16.0 ^16.1 Senechal 1996, p. 171
↑ Luck 2000
↑ ^18.0 ^18.1 Gardner 1997, p. 6
↑ Gardner 1997, p. 19
↑ ^20.0 ^20.1 Gardner 1997, chapter 1
↑ de Bruijn 1981
↑ The P1–P3 notation is taken from Grünbaum & Shephard 1987, section 10.3
↑ Grünbaum & Shephard 1987, section 10.3
↑ Penrose 1978, p. 32
↑ "However, as will be explained momentarily, differently colored pentagons will be considered to be different types of tiles." Austin 2005a; Grünbaum & Shephard 1987, figure 10.3.1, shows the edge modifications needed to yield an aperiodic set of prototiles.
↑ "The rhombus of course tiles periodically, but we are not allowed to join the pieces in this manner." Gardner 1997, pp. 6–7
↑ ^27.0 ^27.1 ^27.2 ^27.3 ^27.4 Grünbaum & Shephard 1987, pp. 537– 547
↑ ^28.0 ^28.1 Senechal 1996, p. 173
↑ ^29.0 ^29.1 Gardner 1997, p. 8
↑ Gardner 1997, pp. 10–11
↑ Gardner 1997, p. 12
↑ Senechal 1996, p. 178
↑ Gardner 1997, p. 9
↑ Gardner 1997, p. 27
↑ Grünbaum & Shephard 1987, p. 543
↑ In Grünbaum & Shephard 1997, the term "inflation" is used where other authors would use "deflation" (followed by rescaling). The terms "composition" and "decomposition", which many authors also use, are less ambiguous.
↑ Penrose 1978, p. 32
↑ Grünbaum & Shephard 1997, p. 546
↑ Senechal 1996, pp. 157–158
↑ ^40.0 ^40.1 ^40.2 ^40.3 Austin 2005b
↑ Senechal 1996, p. 183
↑ Gardner 1997, p. 7
↑ Austin 2005b
↑ Senechal 1996, p. 183
↑ "... any finite patch that we choose in a tiling will lie inside a single inflated tile if we continue moving far enough up in the inflation hierarchy. This means that anywhere that tile occurs at that level in the hierarchy, our original patch must also occur in the original tiling. Therefore, the patch will occur infinitely often in the original tiling and, in fact, in every other tiling as well." Austin 2005a
↑ ^46.0 ^46.1 Lord & Ranganathan 2001
↑ Gummelt 1996
↑ Steinhardt & Jeong 1996; see also Steinhardt, Paul J., "A New Paradigm for the Structure of Quasicrystals", http://www.physics.princeton.edu/~steinh/quasi/.
↑ Lançon & Billard 1988
↑ Godrèche & Lançon 1992; see also E. Harriss and D. Frettlöh, "Binary", Tilings Encyclopedia, Department of Mathematics, University of Bielefeld, http://tilings.math.uni-bielefeld.de/tilings/substitution_rules/binary.
↑ Zaslavskiĭ et al. 1988; Makovicky 1992
↑ Prange, Sebastian R.; Peter J. Lu (2009-09-01). "The Tiles of Infinity". Saudi Aramco World (Aramco Services Company): pp. 24–31. http://www.saudiaramcoworld.com/issue/200905/the.tiles.of.infinity.htm. Retrieved 2010-02-22.
↑ Lu & Steinhardt 2007
↑ Kemp 2005
↑ Ostromoukhov, Donohue & Jodoin 2004

References

Primary sources

Berger, R. (1966), The undecidability of the domino problem, Memoirs of the American Mathematical Society, 66 .
de Bruijn, N. G. (1981), "Algebraic theory of Penrose's nonperiodic tilings of the plane, I, II" (PDF), Indagationes mathematicae 43 (1): 39–66, http://alexandria.tue.nl/repository/freearticles/597566.pdf .
Gummelt, Petra (1996), "Penrose tilings as coverings of congruent decagons", Geometriae Dedicata 62 (1), doi:10.1007/BF00239998 .
Penrose, Roger (1974), "Role of aesthetics in pure and applied research", Bulletin of the Institute of Mathematics and its Applications 10: 266ff .
US 4133152, Penrose, Roger, "Set of tiles for covering a surface", published 1976-06-24, issued 1979-01-09 .
Robinson, R.M. (1971), "Undecidability and nonperiodicity for tilings of the plane", Inventiones Mathematicae 12: 177–190, doi:10.1007/BF01418780 .
Schechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. (1984), "Metallic Phase with long-range orientational order and no translational symmetry", Physical Review Letters 53: 1951–1953, doi:10.1103/PhysRevLett.53.1951
Wang, H. (1961), "Proving theorems by pattern recognition II", Bell Systems Technical Journal 40: 1–42 .

Secondary sources

Austin, David (2005a), "Penrose Tiles Talk Across Miles", Feature Column (Providence: American Mathematical Society), http://www.ams.org/featurecolumn/archive/penrose.html .
Austin, David (2005b), "Penrose Tilings Tied up in Ribbons", Feature Column (Providence: American Mathematical Society), http://www.ams.org/featurecolumn/archive/ribbons.html .
Culik, Karel; Kari, Jarkko (1997), On aperiodic sets of Wang tiles, Lecture Notes in Computer Science, 1337, pp. 153–162, doi:10.1007/BFb0052084
Gardner, Martin (1997), Penrose Tiles to Trapdoor Ciphers, Cambridge University Press, ISBN 978-0883855218 . (First published by W. H. Freeman, New York (1989), ISBN 978-0716719861.)
- Chapter 1 (pp. 1–18) is a reprint of Gardner, Martin (January 1977), "Extraordinary nonperiodic tiling that enriches the theory of tiles", Scientific American 236: 110–121 .
Godrèche, C; Lançon, F. (1992), "A simple example of a non-Pisot tiling with five-fold symmetry", Journal de Physique I 2: 207–220, doi:10.1051/jp1:1992134, http://www.edpsciences.org/10.1051/jp1:1992134 .
Grünbaum, Branko; Shephard, G. C. (1987), Tilings and Patterns, New York: W. H. Freeman, ISBN 978-716711933 .
Kemp, Martin (2005), "Science in culture: A trick of the tiles", Nature 436: 332, doi:10.1038/436332a .
Lançon, Frédéric; Billard, Luc (1988), "Two-dimensional system with a quasi-crystalline ground state", Journal de Physique 4: 249–256, doi:10.1051/jphys:01988004902024900, http://inac.cea.fr/sp2m/L_Sim/Publications/1988/Lancon-Billard-1988-binary_tilings.pdf .
Lord, E.A.; Ranganathan, S. (2001), "The Gummelt decagon as a 'quasi unit cell'", Acta Crystallographica A57: 531–539, doi:10.1107/S0108767301007504, http://materials.iisc.ernet.in/~lord/webfiles/actagum.pdf
Lu, Peter J.; Steinhardt, Paul J. (2007), "Decagonal and Quasi-crystalline Tilings in Medieval Islamic Architecture", Science 315 (5815): 1106–1110, doi:10.1126/science.1135491, PMID 17322056, http://www.physics.harvard.edu/~plu/publications/Science_315_1106_2007.pdf .
Luck, R. (2000), "Dürer-Kepler-Penrose: the development of pentagonal tilings", Materials Science and Engineering 294 (6): 263–267 .
Ostromoukhov, Victor; Donohue, Charles; Jodoin, Pierre-Marc (2004), "Fast Hierarchical Importance Sampling with Blue Noise Properties", ACM Transactions on Graphics (ACM Press) 23 (3): 488–495, doi:10.1145/1015706.1015750, http://www.iro.umontreal.ca/~ostrom/ImportanceSampling/ .
Makovicky, E. (1992), "800-year-old pentagonal tiling from Maragha, Iran, and the new varieties of aperiodic tiling it inspired", in I. Hargittai, Fivefold Symmetry, Singapore–London: World Scientific, pp. 67–86 .
Penrose, Roger (1978), "Pentaplexity", Eureka 39: 16–22 . (Page numbers cited here are from the reproduction as Penrose, R. (1979/80), "Pentaplexity: A class of non-periodic tilings of the plane", The Mathematical Intelligencer 2: 32–37, doi:10.1007/BF03024384 .)
Senechal, Marjorie (1996), Quasicrystals and geometry, Cambridge University Press, ISBN 978-0521575416 .
Steinhardt, Paul J.; Jeong, Hyeong-Chai (1996), "A simpler approach to Penrose tiling with implications for quasicrystal formation", Nature 382 (01 August): 431–433, doi:10.1038/382431a0, http://www.nature.com/nature/journal/v382/n6590/abs/382431a0.html .
Zaslavskiĭ, G.M.; Sagdeev, Roal'd Z.; Usikov, D.A.; Chernikov, A.A. (1988), "Minimal chaos, stochastic web and structures of quasicrystal symmetry", Soviet Physics Uspekhi 31: 887–915, doi:10.1070/PU1988v031n10ABEH005632 .

External links

There are many internet resources related to Penrose tilings; the following is a selection.

Weisstein, Eric W., "Penrose Tiles" from MathWorld.
John Savard, "Penrose Tilings", quadibloc.com, http://www.quadibloc.com/math/pen01.htm, retrieved 2009-11-28.
Eric Hwang, "Penrose Tiling", intendo.net, http://intendo.net/penrose/info.html, retrieved 2009-11-28.
E. Harriss and D. Frettlöh, "Penrose Rhomb", Tilings Encyclopedia, Department of Mathematics, University of Bielefeld, http://tilings.math.uni-bielefeld.de/substitution_rules/penrose_rhomb, retrieved 2009-11-28.
Kevin Brown, "On de Bruijn Grids and Tilings", mathpages.com, http://www.mathpages.com/home/kmath621/kmath621.htm, retrieved 2009-11-28.
David Eppstein, "Penrose Tiles", The Geometry Junkyard, www.ics.uci.edu/~eppstein, http://www.ics.uci.edu/~eppstein/junkyard/penrose.html, retrieved 2009-11-28. This has a list of additional resources.
William Chow, "Penrose tile in architecture", http://www.eschertile.com/penrose.htm, retrieved 2009-12-28.